2016-08-03 • 自定义View,Matrix • View times.

安卓自定义View进阶-Matrix原理

本文内容偏向理论，和画布操作有重叠的部分，本文会让你更加深入的了解其中的原理。

本篇的主角Matrix，是一个一直在后台默默工作的劳动模范，虽然我们所有看到View背后都有着Matrix的功劳，但我们却很少见到它，本篇我们就看看它是何方神圣吧。

由于Google已经对这一部分已经做了很好的封装，所以跳过本部分对实际开发影响并不会太大，不想深究的粗略浏览即可，下一篇中将会详细讲解Matrix的具体用法和技巧。

⚠️ 警告：测试本文章示例之前请关闭硬件加速。

Matrix简介

Matrix是一个矩阵，主要功能是坐标映射，数值转换。

它看起来大概是下面这样:

$\left [ \begin{matrix} MSCALE\_X & MSKEW\_X & MTRANS\_X \ \ MSKEW\_Y & MSCALE\_Y & MTRANS\_Y \ \ MPERSP\_0 & MPERSP\_1 & MPERSP\_2 \end{1} \right ]$

Matrix作用就是坐标映射，那么为什么需要Matrix呢? 举一个简单的例子:

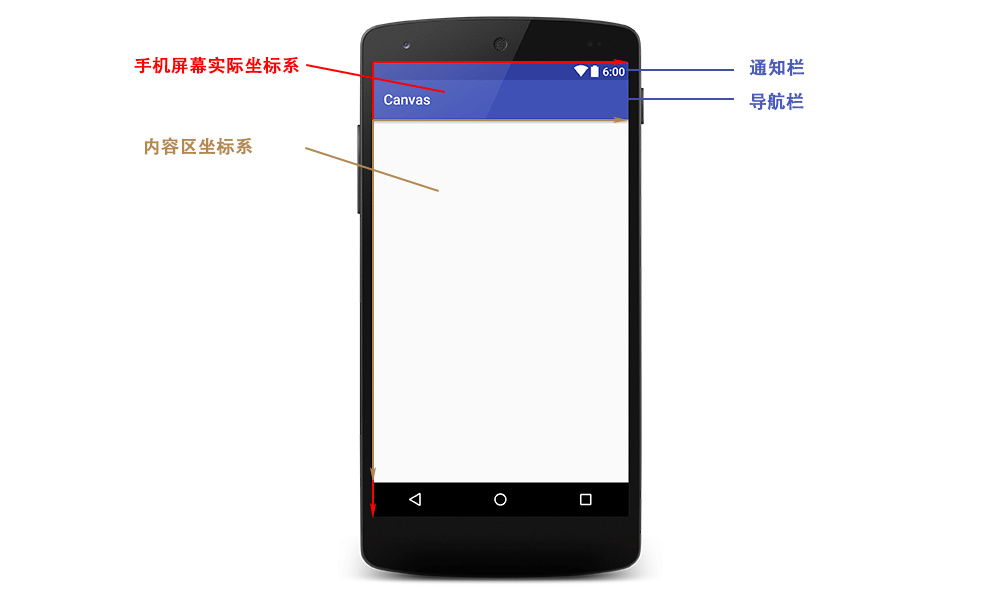
我的的手机屏幕作为物理设备，其物理坐标系是从左上角开始的，但我们在开发的时候通常不会使用这一坐标系，而是使用内容区的坐标系。

以下图为例，我们的内容区和屏幕坐标系还相差一个通知栏加一个标题栏的距离，所以两者是不重合的，我们在内容区的坐标系中的内容最终绘制的时候肯定要转换为实际的物理坐标系来绘制，Matrix在此处的作用就是转换这些数值。

假设通知栏高度为20像素，导航栏高度为40像素,那么我们在内容区的(0，0)位置绘制一个点，最终就要转化为在实际坐标系中的(0，60)位置绘制一个点。

以上是仅作为一个简单的示例，实际上不论2D还是3D，我们要将图形显示在屏幕上，都离不开Matrix，所以说Matrix是一个在背后辛勤工作的劳模。

Matrix特点

作用范围更广，Matrix在View，图片，动画效果等各个方面均有运用，相比与之前讲解等画布操作应用范围更广。
更加灵活，画布操作是对Matrix的封装，Matrix作为更接近底层的东西，必然要比画布操作更加灵活。
封装很好，Matrix本身对各个方法就做了很好的封装，让开发者可以很方便的操作Matrix。
难以深入理解，很难理解中各个数值的意义，以及操作规律，如果不了解矩阵，也很难理解前乘，后乘。

常见误解

1.认为Matrix最下面的一行的三个参数(MPERSP_0、MPERSP_1、MPERSP_2)没有什么太大的作用，在这里只是为了凑数。

实际上最后一行参数在3D变换中有着至关重要的作用，这一点会在后面中Camera一文中详细介绍。

2.最后一个参数MPERSP_2被解释为scale

的确，更改MPERSP_2的值能够达到类似缩放的效果，但这是因为齐次坐标的缘故，并非这个参数的实际功能。

Matrix基本原理

Matrix 是一个矩阵，最根本的作用就是坐标转换，下面我们就看看几种常见变换的原理:

我们所用到的变换均属于仿射变换，仿射变换是线性变换(缩放，旋转，错切) 和平移变换(平移) 的复合，由于这些概念对于我们作用并不大，此处不过多介绍，有兴趣可自行了解。

基本变换有4种: 平移(translate)、缩放(scale)、旋转(rotate) 和错切(skew)。

下面我们看一下四种变换都是由哪些参数控制的。

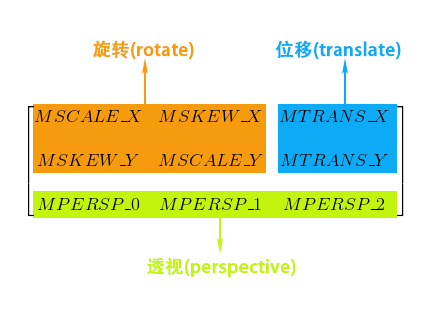
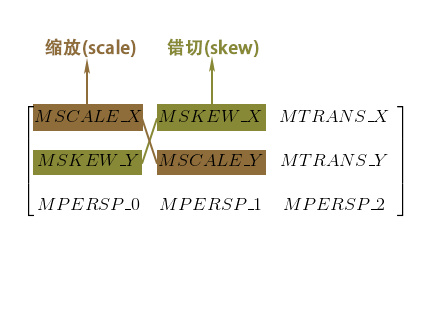
从上图可以看到最后三个参数是控制透视的，这三个参数主要在3D效果中运用，通常为(0, 0, 1)，不在本篇讨论范围内，暂不过多叙述，会在之后对文章中详述其作用。

由于我们以下大部分的计算都是基于矩阵乘法规则，如果你已经把线性代数还给了老师，请参考一下这里: 维基百科-矩阵乘法

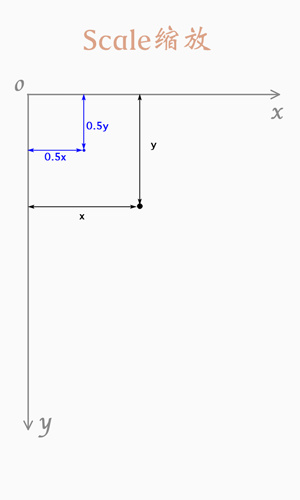
1.缩放(Scale)

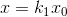
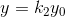
用矩阵表示:

$\left [ \begin{matrix} x\\ y\\ 1 \end{1} \right ] = \left [ \begin{matrix} k_1 & 0 & 0 \\ 0 & k_2 & 0 \\ 0 & 0 & 1 \end{1} \right ] \left [ \begin{matrix} x_0 \\ y_0 \\ 1 \end{1} \right ]$

你可能注意到了，我们坐标多了一个1，这是使用了齐次坐标系的缘故，在数学中我们的点和向量都是这样表示的(x, y)，两者看起来一样，计算机无法区分，为此让计算机也可以区分它们，增加了一个标志位，增加之后看起来是这样:

(x, y, 1) - 点
(x, y, 0) - 向量

另外，齐次坐标具有等比的性质，(2,3,1)、(4,6,2)…(2N,3N,N)表示的均是(2,3)这一个点。(将MPERSP_2解释为scale这一误解就源于此)。

图例：

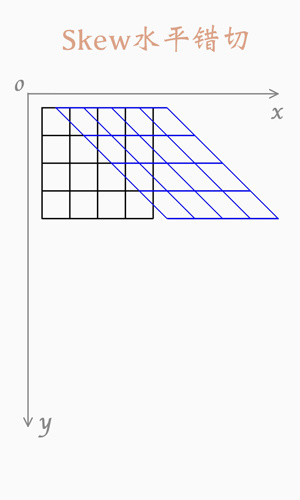
2.错切(Skew)

错切存在两种特殊错切，水平错切(平行X轴)和垂直错切(平行Y轴)。

水平错切

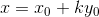
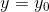
用矩阵表示:

$\left [ \begin{matrix} x\\ y\\ 1 \end{1} \right ] = \left [ \begin{matrix} 1 & k & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{1} \right ] \left [ \begin{matrix} x_0\\ y_0\\ 1 \end{1} \right ]$

图例:

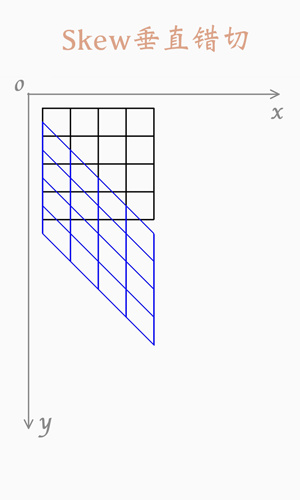
垂直错切

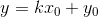
用矩阵表示:

$\left [ \begin{matrix} x\\ y\\ 1 \end{1} \right ] = \left [ \begin{matrix} 1 & 0 & 0 \\ k & 1 & 0 \\ 0 & 0 & 1 \end{1} \right ] \left [ \begin{matrix} x_0\\ y_0\\ 1 \end{1} \right ]$

图例:

复合错切

水平错切和垂直错切的复合。

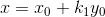
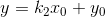
用矩阵表示:

$\left [ \begin{matrix} x\\ y\\ 1 \end{1} \right ] = \left [ \begin{matrix} 1 & k_1 & 0 \\ k_2 & 1 & 0 \\ 0 & 0 & 1 \end{1} \right ] \left [ \begin{matrix} x_0\\ y_0\\ 1 \end{1} \right ]$

图例:

3.旋转(Rotate)

假定一个点 A(x₀, y₀) ,距离原点距离为 r, 与水平轴夹角为 α 度, 绕原点旋转 θ 度, 旋转后为点 B(x, y) 如下:

$x_0 = r \cdot cos \alpha$

$y_0 = r \cdot sin \alpha$

$x = r \cdot cos( \alpha + \theta) = r \cdot cos \alpha \cdot cos \theta - r \cdot sin \alpha \cdot sin \theta = x_0 \cdot cos \theta - y_0 \cdot sin \theta$

$y = r \cdot sin( \alpha + \theta) = r \cdot sin \alpha \cdot cos \theta + r \cdot cos \alpha \cdot sin \theta = y_0 \cdot cos \theta + x_0 \cdot sin \theta$

用矩阵表示:

$\left [ \begin{matrix} x\\ y\\ 1 \end{1} \right ] = \left [ \begin{matrix} cos(\theta) & -sin(\theta) & 0 \\ sin(\theta) & cos(\theta) & 0 \\ 0 & 0 & 1 \end{1} \right ] . \left [ \begin{matrix} x_0\\ y_0\\ 1 \end{1} \right ]$

图例:

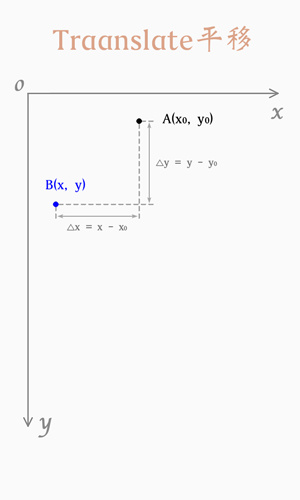
4.平移(Translate)

此处也是使用齐次坐标的优点体现之一，实际上前面的三个操作使用 2x2 的矩阵也能满足需求，但是使用 2x2 的矩阵，无法将平移操作加入其中，而将坐标扩展为齐次坐标后，将矩阵扩展为 3x3 就可以将算法统一，四种算法均可以使用矩阵乘法完成。

$x = x_0 + \Delta x$

$y = y_0 + \Delta y$

用矩阵表示:

$\left [ \begin{matrix} x\\ y\\ 1 \end{1} \right ] = \left [ \begin{matrix} 1 & 0 & \Delta x \\ 0 & 1 & \Delta y \\ 0 & 0 & 1 \end{1} \right ] . \left [ \begin{matrix} x_0\\ y_0\\ 1 \end{1} \right ]$

图例:

Matrix复合原理

其实Matrix的多种复合操作都是使用矩阵乘法实现的，从原理上理解很简单，但是，使用矩阵乘法也有其弱点，后面的操作可能会影响到前面到操作，所以在构造Matrix时顺序很重要。

我们常用的四大变换操作，每一种操作在Matrix均有三类,前乘(pre)，后乘(post)和设置(set)，可以参见文末对Matrix方法表，由于矩阵乘法不满足交换律，所以前乘(pre)，后乘(post)和设置(set)的区别还是很大的。

前乘(pre)

前乘相当于矩阵的右乘：

$M' = M \cdot S$

这表示一个矩阵与一个特殊矩阵前乘后构造出结果矩阵。

后乘(post)

后乘相当于矩阵的左乘：

$M' = S \cdot M$

这表示一个矩阵与一个特殊矩阵后乘后构造出结果矩阵。

设置(set)

设置使用的不是矩阵乘法，而是直接覆盖掉原来的数值，所以，使用设置可能会导致之前的操作失效。

组合

关于 Matrix 的文章终有一个问题，就是 pre 和 post 这一部分的理论非常别扭，国内大多数文章都是这样的，看起来貌似是对的但很难理解，部分内容违背直觉。

我由于也受到了这些文章的影响，自然而然的继承了这一理论，直到在评论区有一位小伙伴提出了一个问题，才让我重新审视了这一部分的内容，并进行了一定反思。

经过良久的思考之后，我决定抛弃国内大部分文章的那套理论和结论，只用严谨的数学逻辑和程序逻辑来阐述这一部分的理论，也许仍有疏漏，如有发现请指正。

首先澄清两个错误结论，记住，是错误结论，错误结论，错误结论。

错误结论一：pre 是顺序执行，post 是逆序执行。

这个结论很具有迷惑性，因为这个结论并非是完全错误的，你很容易就能证明这个结论，例如下面这样：

// 第一段 pre  顺序执行，先平移(T)后旋转(R)
Matrix matrix = new Matrix();
matrix.preTranslate(pivotX,pivotY);
matrix.preRotate(angle);
Log.e("Matrix", matrix.toShortString());

// 第二段 post 逆序执行，先平移(T)后旋转(R)
Matrix matrix = new Matrix();
matrix.postRotate(angle);
matrix.postTranslate(pivotX,pivotY)
Log.e("Matrix", matrix.toShortString());

这两段代码最终结果是等价的，于是轻松证得这个结论的正确性，但事实真是这样么？

首先，从数学角度分析，pre 和 post 就是右乘或者左乘的区别，其次，它们不可能实际影响运算顺序(程序执行顺序)。以上这两段代码等价也仅仅是因为最终化简公式一样而已。

设原始矩阵为 M，平移为 T ，旋转为 R ，单位矩阵为 I ，最终结果为 M’

矩阵乘法不满足交换律，即 A*B ≠ B*A

矩阵乘法满足结合律，即 (A*B)*C = A*(B*C)

矩阵与单位矩阵相乘结果不变，即 A * I = A

由于上面例子中原始矩阵(M)是一个单位矩阵(I)，所以可得：

// 第一段 pre
M' = (M*T)*R = I*T*R = T*R

// 第二段 post
M' = T*(R*M) = T*R*I = T*R

由于两者最终的化简公式是相同的，所以两者是等价的，但是，这结论不具备普适性。

即原始矩阵不为单位矩阵的时候，两者无法化简为相同的公式，结果自然也会不同。另外，执行顺序就是程序书写顺序，不存在所谓的正序逆序。

错误结论二：pre 是先执行，而 post 是后执行。

这一条结论比上一条更离谱。

之所以产生这个错误完全是因为写文章的人懂英语。

pre  ：先，和 before 相似。
post ：后，和 after  相似。

所以就得出了 pre 先执行，而 post 后执行这一说法，但从严谨的数学和程序角度来分析，完全是不可能的，还是上面所说的，pre 和 post 不能影响程序执行顺序，而程序每执行一条语句都会得出一个确定的结果，所以，它根本不能控制先后执行，属于完全扯淡型。

如果非要用这套理论强行解释的话，反而看起来像是 post 先执行，例如：

matrix.preRotate(angle);
matrix.postTranslate(pivotX,pivotY);

同样化简公式：

// 矩阵乘法满足结合律
M‘ = T*(M*R) = T*M*R = (T*M)*R

从实际上来说，由于矩阵乘法满足结合律，所以不论你说是靠右先执行还是靠左先执行，从结果上来说都没有错。

之前基于这条错误的结论我进行了一次错误的证明：

(这段内容注定要成为我写作历程中不可抹灭的耻辱，既然是公开文章，就应该对读者负责，虽然我在发表每一篇文章之前都竭力的求证其中的问题，各种细节，避免出现这种错误，但终究还是留下了这样一段内容，在此我诚挚的向我所有的读者道歉。)

关注我的读者请尽量看我在个人博客和 GitHub 发布的版本，这两个平台都在博文修复计划之内，有任何错误或者纰漏，都会首先修复这两个平台的文章。另外，所有进行修复过的文章都会在我的微博 @GcsSloop 重新发布说明，关注我的微博可以第一时间得到博文更新或者修复的消息。

以下是错误证明：

在实际操作中，我们每一步操作都会得出准确的计算结果，但是为什么还会用存在先后的说法? 难道真的能够用pre和post影响计算顺序? 实则不然，下面我们用一个例子说明:
Matrix matrix = new Matrix();
matrix.postScale(0.5f, 0.8f);
matrix.preTranslate(1000, 1000);
Log.e(TAG, "MatrixTest" + matrix.toShortString());
在上面的操作中，如果按照正常的思路，先缩放，后平移，缩放操作执行在前，不会影响到后续的平移操作，但是执行结果却发现平移距离变成了(500， 800)。

在上面例子中，计算顺序是没有问题的，先计算的缩放，然后计算的平移，而缩放影响到平移则是因为前一步缩放后的结果矩阵右乘了平移矩阵，这是符合矩阵乘法的运算规律的，也就是说缩放操作虽然在前却影响到了平移操作，相当于先执行了平移操作，然后执行的缩放操作，因此才有pre操作会先执行，而post操作会后执行这一说法。

上面的论证是完全错误的，因为可以轻松举出反例：
Matrix matrix = new Matrix();
matrix.preScale(0.5f, 0.8f);
matrix.preTranslate(1000, 1000);
Log.e(TAG, "MatrixTest" + matrix.toShortString());
反例中，虽然将 postScale 改为了 preScale ，但两者结果是完全相同的，所以先后论根本就是错误的。

他们结果相同是因为最终化简公式是相同的，都是 S*T

之所以平移距离是 MTRANS_X = 500，MTRANS_Y = 800，那是因为执行 Translate 之前 Matrix 已经具有了一个缩放比例。在右乘的时候影响到了具体的数值计算，可以用矩阵乘法计算一下。

$\left [ \begin{matrix} 0.5 & 0 & 0 \\ 0 & 0.8 & 0 \\ 0 & 0 & 1 \end{1} \right ] \cdot \left [ \begin{matrix} 1 & 0 & 1000 \\ 0 & 1 & 1000 \\ 0 & 0 & 1 \end{1} \right ] = \left [ \begin{matrix} 0.5*1+0*0+0*0 & 0.5*0+0*1+0*0 & 0.5*1000+0*1000+0*1\\ 0*1+0.8*0+0*0 & 0*0+0.8*1+0*1 & 0*1000+0.8*1000+0*1\\ 0*1+0*0+1*0 & 0*0+0*1+1*0 & 0*1000+0*1000+1*1 \end{1} \right ]$

最终结果为：

$\left [ \begin{matrix} 0.5 & 0 & 500\\ 0 & 0.8 & 800\\ 0 & 0 & 1 \end{1} \right ]$

当 T*S 的时候，缩放比例则不会影响到 MTRANS_X 和 MTRANS_Y ，具体可以使用矩阵乘法自己计算一遍。

如何理解和使用 pre 和 post ？

不要去管什么先后论，顺序论，就按照最基本的矩阵乘法理解。

pre  : 右乘， M‘ = M*A
post : 左乘， M’ = A*M

那么如何使用？

正确使用方式就是先构造正常的 Matrix 乘法顺序，之后根据情况使用 pre 和 post 来把这个顺序实现。

还是用一个最简单的例子理解，假设需要围绕某一点旋转。

可以用这个方法 xxxRotate(angle, pivotX, pivotY) ,由于我们这里需要组合构造一个 Matrix，所以不直接使用这个方法。

首先，有两条基本定理：

所有的操作(旋转、平移、缩放、错切)默认都是以坐标原点为基准点的。
之前操作的坐标系状态会保留，并且影响到后续状态。

基于这两条基本定理，我们可以推算出要基于某一个点进行旋转需要如下步骤：

1. 先将坐标系原点移动到指定位置，使用平移 T
2. 对坐标系进行旋转，使用旋转 S (围绕原点旋转)
3. 再将坐标系平移回原来位置，使用平移 -T

具体公式如下：

M 为原始矩阵，是一个单位矩阵， M‘ 为结果矩阵， T 为平移， R为旋转

M' = M*T*R*-T = T*R*-T

按照公式写出来的伪代码如下：

Matrix matrix = new Matrix();
matrix.preTranslate(pivotX,pivotY);
matrix.preRotate(angle);
matrix.preTranslate(-pivotX, -pivotY);

围绕某一点操作可以拓展为通用情况，即：

Matrix matrix = new Matrix();
matrix.preTranslate(pivotX,pivotY);
// 各种操作，旋转，缩放，错切等，可以执行多次。
matrix.preTranslate(-pivotX, -pivotY);

公式为：

M' = M*T* ... *-T = T* ... *-T

但是这种方式，两个调整中心的平移函数就拉的太开了，所以通常采用这种写法：

Matrix matrix = new Matrix();
// 各种操作，旋转，缩放，错切等，可以执行多次。
matrix.postTranslate(pivotX,pivotY);
matrix.preTranslate(-pivotX, -pivotY);

这样公式为：

M' = T*M* ... *-T = T* ... *-T

可以看到最终化简结果是相同的。

所以说，pre 和 post 就是用来调整乘法顺序的，正常情况下应当正向进行构建出乘法顺序公式，之后根据实际情况调整书写即可。

在构造 Matrix 时，个人建议尽量使用一种乘法，前乘或者后乘，这样操作顺序容易确定，出现问题也比较容易排查。当然，由于矩阵乘法不满足交换律，前乘和后乘的结果是不同的，使用时应结合具体情景分析使用。

下面我们用不同对方式来构造一个相同的矩阵:

注意:

1.由于矩阵乘法不满足交换律，请保证使用初始矩阵(Initial Matrix)，否则可能导致运算结果不同。
2.注意构造顺序，顺序是会影响结果的。
3.Initial Matrix是指new出来的新矩阵，或者reset后的矩阵，是一个单位矩阵。

1.仅用pre：

// 使用pre， M' = M*T*S = T*S
Matrix m ＝ new Matrix();
m.reset();
m.preTranslate(tx, ty); 
m.preScale(sx, sy);

用矩阵表示:

$\left [ \begin{matrix} & &\\ & Result Matrix &\\ & & \end{1} \right ] = \left [ \begin{matrix} & &\\ & Initial Matrix &\\ & & \end{1} \right ] \cdot \left [ \begin{matrix} 1 & 0 & \Delta x \\ 0 & 1 & \Delta y \\ 0 & 0 & 1 \end{1} \right ] \cdot \left [ \begin{matrix} sx & 0 & 0\\ 0 & sy & 0\\ 0 & 0 & 1 \end{1} \right ]$

2.仅用post:

// 使用post， M‘ = T*S*M = T*S
Matrix m ＝ new Matrix();
m.reset();
m.postScale(sx, sy);  //，越靠前越先执行。
m.postTranslate(tx, ty);

用矩阵表示:

$\left [ \begin{matrix} & &\\ & Result Matrix &\\ & & \end{1} \right ] = \left [ \begin{matrix} 1 & 0 & \Delta x \\ 0 & 1 & \Delta y \\ 0 & 0 & 1 \end{1} \right ] \cdot \left [ \begin{matrix} sx & 0 & 0\\ 0 & sy & 0\\ 0 & 0 & 1 \end{1} \right ] \cdot \left [ \begin{matrix} & &\\ & Initial Matrix &\\ & & \end{1} \right ]$

3.混合:

// 混合 M‘ = T*M*S = T*S
Matrix m ＝ new Matrix();
m.reset();
m.preScale(sx, sy);  
m.postTranslate(tx, ty);

或:

// 混合 M‘ = T*M*S = T*S
Matrix m ＝ new Matrix();
m.reset();
m.postTranslate(tx, ty);
m.preScale(sx, sy);

由于此处只有两步操作，且指定了先后，所以代码上交换并不会影响结果。

用矩阵表示:

$\left [ \begin{matrix} & &\\ & Result Matrix &\\ & & \end{1} \right ] = \left [ \begin{matrix} 1 & 0 & \Delta x \\ 0 & 1 & \Delta y \\ 0 & 0 & 1 \end{1} \right ] \cdot \left [ \begin{matrix} & &\\ & Initial Matrix &\\ & & \end{1} \right ] \cdot \left [ \begin{matrix} sx & 0 & 0\\ 0 & sy & 0\\ 0 & 0 & 1 \end{1} \right ]$

注意: 由于矩阵乘法不满足交换律，请保证初始矩阵为单位矩阵，如果初始矩阵不为单位矩阵，则导致运算结果不同。

上面虽然用了很多不同的写法，但最终的化简公式是一样的，这些不同的写法，都是根据同一个公式反向推算出来的。

Matrix方法表

这个方法表，暂时放到这里让大家看看，方法的使用讲解放在下一篇文章中。

方法类别	相关API	摘要
基本方法	equals hashCode toString toShortString	比较、获取哈希值、转换为字符串
数值操作	set reset setValues getValues	设置、重置、设置数值、获取数值
数值计算	mapPoints mapRadius mapRect mapVectors	计算变换后的数值
设置(set)	setConcat setRotate setScale setSkew setTranslate	设置变换
前乘(pre)	preConcat preRotate preScale preSkew preTranslate	前乘变换
后乘(post)	postConcat postRotate postScale postSkew postTranslate	后乘变换
特殊方法	setPolyToPoly setRectToRect rectStaysRect setSinCos	一些特殊操作
矩阵相关	invert isAffine isIdentity	求逆矩阵、是否为仿射矩阵、是否为单位矩阵 …

总结

对于Matrix重在理解，理解了其中的原理之后用起来将会更加得心应手。

学完了本篇之后，推荐配合鸿洋大大的视频课程打造个性的图片预览与多点触控食用，定然能够让你对Matrix对理解更上一层楼。

由于个人水平有限，文章中可能会出现错误，如果你觉得哪一部分有错误，或者发现了错别字等内容，欢迎在评论区告诉我，另外，据说关注作者微博不仅能第一时间收到新文章消息，还能变帅哦。

About

本系列相关文章

作者微博: GcsSloop

参考资料

Matrix
Android中图像变换Matrix的原理、代码验证和应用
 Android中关于矩阵（Matrix）前乘后乘的一些认识
 维基百科-仿射变换
 维基百科-齐次坐标
 维基百科-线性映射
 齐次坐标系入门级思考
 仿射变换与齐次坐标

GcsSloop

安卓自定义View进阶-Matrix原理

⚠️ 警告：测试本文章示例之前请关闭硬件加速。

Matrix简介

Matrix特点

常见误解

Matrix基本原理

1.缩放(Scale)

2.错切(Skew)

水平错切

垂直错切

复合错切

3.旋转(Rotate)

4.平移(Translate)

Matrix复合原理

前乘(pre)

后乘(post)

设置(set)

组合

错误结论一：pre 是顺序执行，post 是逆序执行。

错误结论二：pre 是先执行，而 post 是后执行。

以下是错误证明：

如何理解和使用 pre 和 post ？

下面我们用不同对方式来构造一个相同的矩阵:

1.仅用pre：

2.仅用post:

3.混合:

Matrix方法表

总结

About

参考资料

如果你觉得我的文章对你有帮助的话，欢迎赞助一些服务器费用!

欢迎关注我的微信公众号

ArrayList与LinkedList遍历性能比较

安卓自定义View进阶-PathMeasure